概要
将棋プログラムの製作においてある局面からの読むべき手を選択する方法として、より人間らしい思考方法を取り入れるために一度探索をした後、その結果を反省するような指し手の生成について述べる。
In this paper, a new method of move-generation
in a Shogi(Japanese chess) program is described. In this method,
which is operated in the way of human thinking, a program
firstly obtains the best sequence, and then
examines itself. Since the average branching factor of Shogi is
usually over 100, a Shogi program
cannot use the brute-force method which works successfully in
all the chess programs. It is therefore necessary for a Shogi
program to have methods which can select the effective moves from
all the possibilities. The method which is introduced in this
paper is one of those methods.
将棋プログラムにおいて重要なことは正しい手を探索すること、そしてその読んだ後の局面が良いと正しく判断できることである。
前者において将棋は可能な手が平均100前後なので、そのまま全ての指し手を探索したのでは得られる局面の数が幾何級数的に爆発する。そのため可能な手の中から有効と思われる手のみを抽出してやる必要がある。
本稿では私が作成した将棋プログラム「YSS」について、いかにして探索するべき指し手を定めているかについて述べる。探索した後の局面の善し悪しを決める評価関数については指し手の生成と同様に重要だがここでは触れない。
YSSでは次の様に指し手を分類している。まず、攻める手、受ける手に分ける。攻める手としては駒を取る手、成る手、次に駒を取りに行く手(両取りも含む)に分ける。駒を取りに行く手は、取っても得にならない手や歩を取りに行く手は最初から除外している。(これらの手は浅い深さにおいては別のルーチンで生成する)
それぞれの手について、その移動する升目における敵と味方の利きの数によりミニ・マックスで処理をして仮評価をつけている。ミニ・マックスでの処理の仕方は以下の通りである。
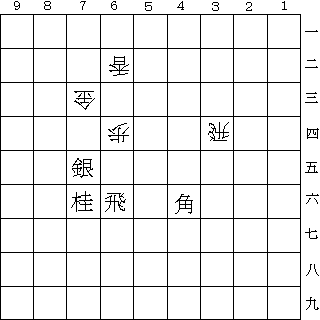
第1図
上手の持駒:なし

下手の持駒:なし
- 表1-
歩 100: 香 330:
桂 380: 銀
500: 金 550 :角
800: 飛 950
第1図において64の歩を取る価値は、駒の価値を表1のように考え、まず駒の交換は価値の低い順に起こると仮定する。この場合は先手は桂、銀、角、飛の順に64に移動し、後手は香、金、飛の順番となる。で最初は先手には64の歩を取るか取らないか選択する権利があり、歩を桂で取ったとすると後手にはその桂を取るか取らずかの権利が同様にある。これを図にすると第2図
のようになる。(図省略)
この図で先手番をマックス局面、後手番をミニ局面として取った時を左側、取らなかった時を右側の枝とすると、最初取らないと当然のごとく価値は0、最初取って次に取り返してこないと歩得なので+100、で取り返しにきた後取らないと歩−桂になるので-280。
このようにして木を作って下から繰り上げると結局歩を取る手の価値は+50となる。
受ける手としては、取られる駒に対して逃げる手、合駒する手、ひもを付ける手、取ろうとする相手の駒を取る、飛角香の利きが足されているなら合駒する、また、駒を打つ手が好手の場合は先にその升目に駒を打つ、利きを付ける手、である。
この他に浅い深さにおいては、歩をたらす手、飛車角を打ち込む手、歩を叩く手、王周辺に駒をぶち込む手、と金などが敵の王に寄って行く手、空き当たりを掛ける手、歩を取りに行く手、カット駒(飛角香ににらまれている駒)への駒当たり、王周辺に利きを付ける手、飛角香の利きを止める手、駒の損得を無視して駒を取る手、ただでも王手をする手、全ての駒に対してでたらめに動く手を2手づつ生成する、といった具合に細分化して処理している。
全ての「手を生成するサブルーチン」において、個々にその重要性から生成する手の数に制限をつけている。
そして、生成された手は全て探索に回している。このため生成する手の数は深さの関数にはなっていない。複雑な局面においては深い局面であっても多くの手を生成する。
逆にあまり手を生成する要因がない局面では、ほとんど手を生成しない。
このため序盤ではすぐに局面が「静か」になってしまうのでほとんど手を読むことなく時間を使わずに指す。
なお、1局面において探索に回す手の最大数は32手としている。32手を超えた場合は個々の指し手の仮評価によって選択する。
これらの指し手生成に共通する致命的欠点は1手の読みに基づいてしか指し手を生成しない点である。つまり考えが浅いのである。例えば桂が取れるので桂を取る手、取られそうなので守る手等である。飛車が追われて殺されるような手を防ぐことは困難であった。
そこで受ける手に対してはより深い意味での(狙いを持った)指し手生成を行う方法を示す。
まず最善の応手を求めてから、その後、その指し手(応手)を反駁する手をそれまでの各深さにおいてさらに生成する。
詳しく言うと、まず上述の指し手の分類に従ってミニ・マックス法(実際はαβ法)で探索を行う。
その結果、最初の局面の評価値と最善の手を見つける。
この時、初手においての最善の手を見つけるだけでなく、その初手を指した後の局面での相手の最善手も求める。
このようにして「自分の最善手、それを指した時の相手の最善手、その時の自分の最善手、・・・」と、お互いに最善の手を指した場合に得られる手順を最善の応手と呼ぶ。
第3図の場合は太線で表したのが最善の応手となる。
その後、この応手の中の自分の手番の手を最初の局面において生成する。これは駒が先に逃げておく時などに有効である[1]。
次に相手の手番の手を防ぐ手、例えば駒が取られるならばその駒が逃げれるような手を生成する。(実際に逃げれるかどうかはその後の読みによって確かめる)
例として第4図を示す。
第4図
後手の持駒:歩二
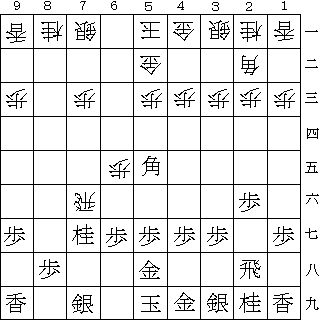
先手の持駒:なし
この局面において先手は何もしないと54歩から角を追われて77の桂をただで取られてしまう。もしこの局面において55の角が存在しないのであれば77の桂が1手で取られることが分かるので78銀、68金等、ひもを付ける手の発見は容易である。
そこでこの局面において先手が、あまり意味のない指し手(端歩を突く等)を指したとする。(実際には1手パスをして処理している)
その結果、先手の手、54歩、46角、77飛成、69玉、という最善の応手を見つける。
そこでこの応手の内、先手番の手ならばその手を、後手番の手ならばそれを咎める手を初手において生成するわけである。
ここでは46角、69玉の2つの手を初手において生成し、後手番の54歩を咎める手(ここでは存在しない)桂を取っての77飛成を防ぐ手を生成する。
この場合77にひもを付ける78銀、68金や、取られる桂が逃げる85桂、65桂を生成する。
またこの場合は桂を取られる手が直前(1手前)ではないので桂の逃げ道を作る手も生成する。(この場合どちらにも動けるので関係ない)
この結果、1手の読みでは分からなかった78銀等の受ける手を見つけることが出来る。
また、これらの手は直前の指手を防ぐ手以外においては盤面が変化して指すことが不可能なことも当然あり得る。その場合は無視する。
実際の探索においては初手だけでなく2手目、3手目、・・・第n手目の深さにおいても許された探索深さの限界まで再帰的に行う。
正しい手を読ませることが重要である事を示す例として第5図をあげる。
第5図
題名:第50手、▲7八飛に△6二飛です。
後手:柿木
後手の持駒:金

先手:YSS
先手の持駒:角
これは第4回コンピュータ将棋選手権における「YSS−柿木将棋」戦において生じた局面である。
この局面においては後手からの26金が角桂両取りで厳しい手であるが後手は62飛と指した。
深く探索するプログラムにおいては26金という手を初手だけでなく3手目、5手目、・・・ともっと深い手番においても生成する。
そのため、相手の受ける手(ここでは26角打や49角)を読んでいない場合、いつでも指せると判断してすぐには指さない場合がある。
つまり、相手の正確な応手を読んでいないために自分の好手をすぐには指さず、防がれてしまうのである。
これも上述の方法により改善できる。
先手が探索の中で62飛と指した後、後手は1手パスをして26金、49角、37金、という最善の応手を見つける。
その結果自分の手番の49角を2手目に生成し、相手の手番の26金、37金を防ぐ手もまた生成する。
これにより、初手に62飛と指した場合、26金が3手目以降に指せなくなることが分かる。
なお、現時点のYSSは直前の相手の好手を防ぐ手のみしか生成していない。
(実戦においてYSSは49角を指したが、これはでたらめに手を生成してたまたま 上手くいった偶然によるものである)
このアルゴリズムにより、一通り読んでみてその結果「6手目に割銀がかかるからあらかじめ飛車を逃げておこう」とか、「角が追われて死ぬから5手後の逃げみちを開けておこう」といった事が可能となってきた。
また、これは攻めにもつながる。例えば「飛車を追い回すと34に逃げられるから、あらかじめ34に歩で利きをつけておこう」といった感じにである。
将棋プログラムでは歩をただで叩いたり、無意味な角での王手等、将来的に見れば損をする手を指すことがしばしばある。
これは地平線効果と呼ばれ、完全には解決しがたい。
最もやっかいなのが絶対手の存在する局面である。
例えば持ち駒に角を持っていて王手がかかる場合、それに対して合駒する手(又は逃げる手)が絶対手となってしまう。
そのため、6手の探索をしているつもりでも4手の探索しか実質していないことになって、読みの深さが短くなってしまう。
この内、駒をただで捨てる手に対してはそれを取る手の探索を無条件に2手延長することによりかなり改善された。
この結果、はっきり負けとなった局面での無意味な駒をただで捨てる王手の連続が減ってすぐに投了することが多くなった。
また終盤で用いる詰将棋ルーチンにおいては無駄な合駒(中合)は読まない、大駒の不成は読まない、大駒を遠くからは打たない、駒損しすぎる場合は打ち切る、捨駒の回数を制限する等の条件をつけ、ハッシュ法[2]と反復深化法を用いることにより高速化している。無論用いるのは実戦においてのみで芸術的な「詰将棋」には使えない。
後、高速化に大きな影響があった例として例えば飛車が逃げるときに逃げる手を2、3手に絞る場合、実際に1手指してみてその局面における駒の取り合いを評価してから評価の高い順に選んだ場合と、実際には盤面を動かさずに単純な評価のみで選んだ場合では前者では評価がより正確だが、それよりも実際に駒を動かすロスの方が大きく、より多くの手を読める後者のほうが成績が良かった。
5.終わりに
将棋プログラムにおける指し手の生成について人間の推論に近いことを探索プログラム中に取り入れることが可能なことを示した。これらの実現には指し手の細かい分類が必要であり、最低限の処理を要する。
今後、将棋プログラムを強くしていくためには評価関数を含め、まだまだ改良が必要であろう。
謝辞
将棋プログラムのアルゴリズムに関して阪下真弘氏には活発な議論をしていただいた。感謝したい。
「参考文献」
[1] 飯田弘之、小谷善行:エキスパートの思考をモデルとしたゲーム木探索の方式、情報処理学会論文誌,
Vol.33, No.11, pp. 1296-1350 (1992)
[2] 伊藤琢巳、野下浩平:「詰め将棋を速く解く2つのプログラム」、情報処理学会第34回プログラミングシンポジウム (1993)
_